CHAPTER 4
DESIGN PROCESS FLOWS AND SOFTWARE TOOLS
The
purpose of this chapter is to:
- Describe the functionality of
design tools, both generic and those appropriate to a field-programmable
gate-array (FPGA)
- Describe some typical examples,
from start to finish, of design process flows, using manufacturer-supplied
cases. For simplicity only single-chip designs will be used at this stage.
We include schematic-based, behavioral-and floorplan-based examples.
4.1 THE
SOFTWARE TOOLBOX
Designing is a very exciting part of
engineering. Leaving aside formal definitions, it is the phase of engineering
where creativity and problem solving play the most important part. These
activities allow explorations of design options by trial and error, engineering
judgment, “guesstimation,” analysis, measurement, simulation, breadboarding,
and so forth. There is normally an overall strategy, however, to guide the
transition from specification to implementation, as discussed in
Chapter 1. What the engineer must do is flesh out
a complete behavioral, structural, and physical description so that a design
can be built and tested. With these often onerous tasks and informal
procedures, we can expect tools to “get in the way” of designing. The purpose
of this chapter is to be informative about the applicability of tools for FPGA
design and suggest fairly loose design process flows. The treatment is based on
taking a simple design example, the 7-segment display driver, through a
behavioral and structural design process. This example is conceptually simple,
but it is a nontrivial 4-input, 7-output function. It is also a standard
transistor-transistor logic (TTL) catalog part, the TTL7446. This serves to
emphasize alternatives in design process flows as well as highlighting the
relevance, or irrelevance, of specific tools.
This treatment is in distinction
to some more conventional approaches, mostly as found in manufacturers’
literature, which often portray the design process as a sequential walk through
a small number of design steps, yielding a perfect result every time.
Another source of confusion is
the plethora of tools available today. This is because the electronic CAD
industry has matured over the last 10 years into a number of sustainable
businesses (see
Chapter 7). The design bottlenecks of the
mid-1970s have been eliminated by structured design techniques embodied in new
tools and often the products of start-up companies. Today such companies are
mature and concentrating on marketing their products. The noise level is
rising, and it is important to be able to identify the functionality of a tool
to assess its relevance to FPGA design.
Table 4–1 enumerates tool types against design
description and level of design abstraction.
As a starting point, let us
examine the primary activities in designing. These may be termed design
capture, design validation, and physical design.
Figure 4–1 shows possible flows between activities
as well as tools that can assist in the processes within activities. Note that
the starting point for designing is the existence of a specification and that
the end point is the production of manufacturing data. Transitions in the flow
are driven by design refinement, yielding acceptable or infeasible designs.
Transitions to revise the specification are allowed.
Figure 4–1. Design process
flows.
Now in the case of FPGAs and our
example, to get into the flow we need a specification. The specification of a
7-segment display driver is intuitively obvious, given a labeling scheme for
the segments (see
Figure 4–2) and no performance or electrical
requirements. It could be, “drive the segments of the display to show the
decimal digits 0–9 from their 4-bit binary representation as input.” Well, how
do tools in a contemporary toolbox help, given this simple specification? The
following sections illustrate process steps.
4.1.1 Design
Capture
All design capture tools provide
functions for capturing design intent. They may capture structural intent,
behavioral intent, or both. They may be graphically based, for example,
schematics, or language based, for example, hardware description language
(HDL).
Figure 4–2. Labeling of
7-segment display.
Behavioral Tools Behavioral
tools address the question “what do I want this circuit to do?” Since the
behavior of a circuit is a mapping between a set of input states and a set of
output states, dependent on internal state (for sequential circuits), then
representations, such as truth tables, logic equations, and state descriptions,
are particularly useful. Truth tables are a perfectly simple and universal
behavioral description. The initial truth table for the display decoder is
shown in
Table 4–2. With the availability of programmable
array logic (PALs), several commercial behavioral HDL notations have emerged as
de facto standards: ABEL, CUPL, PALASM. The PALASM2 form of the same design is
shown in
Figure 4–3. For the established PAL families there
is even a standard file format for specifying fuse maps. In some cases these
can be interpreted as truth tables, but they are really a physical description
of features of a chip.

Synthesis If
behavioral tools only provided methods of describing circuit functions, then
they would be at least useful in refining specifications, assuming the
behavioral description could be animated. To take a first step to a real
manufacturable entity, however, a set of elements with defined behaviors must
be hooked up to make a circuit. Now if the behavioral semantics of these
elements are well understood, for example, in the case of logic gates, 2-level
logic blocks like PLAs, then it is possible to transform a behavioral
description into a structural composition of known parts. This is called synthesis.
Trivial examples would include interpreting a logic diagram as a behavioral and
structural design; mapping a set of logic equations into a PLA; decomposing an
HDL into a set of register-transfer-level interconnected elements. Optimization
is associated with synthesis and is applied to the automatic manipulation of
logic equations to yield an optimal, in some sense, logic-level design. Today
optimization and synthesis products are available from a range of companies.

Figure 4–3. PALASM2 HDL for
display driver. Figure courtesy of Xilinx Inc. ©Xilinx, Inc. 1989. All rights
reserved.
Structural Tools Structural
tools address capturing the design statement, “I think this interconnection of
units will exhibit the required behavior.” This is the more traditional design
metaphor, and it assumes the engineer is using knowledge of the behavior of
units, experience, judgment, and so forth, in making a plausible design
statement. Historically, this metaphor has always been supported by schematic
tools. In the case of the display driver, a schematic is shown in
Figure 4–4. This nonobvious design is structured
across three levels of logic. The top level drawing uses a left-to-right signal
flow convention.
Hardware Description Languages In
recent times HDLs like VHDL
[Mazor93] and Verilog have emerged as alternative
textual tools for design capture. Their present existence is based on work over
a long period of time to discover how to exploit the power of programming notations
in hardware design. In designs with repeated structures or conditional
structures, there are obvious advantages in using HDL descriptions, assuming
HDL compilers exist that can sensibly instantiate the design to a low-level
netlist form.
This type of HDL, compared to
the purely behavioral type, can be used for structural design and/or behavioral
design. The most common use is as a structural design tool to allow more rapid
generation of netlist data, that is, descriptions of interconnections of gate level
elements.
Figure 4–5 shows a VHDL description of the
schematics.
4.1.2 Tools
for Design Validation
Validation tools address the question
“what will this (structural) design do and how fast will it do it?” A broad
spectrum of simulator products, from circuit-level simulators, which solve the
underlying differential equations by numerical methods, to ad hoc
functional simulators in a high-level programming language, can be used.
However, with the emergence of component families at mediumscale integration
(MSI), large-scale integration (LSI), and very-large-scale integration (VLSI)
levels, logic level simulators have become the key design validation tools.
Since FPGAs by and large deliver gate level functions, logic level simulators
are particularly relevant.
Logic simulators are good at
answering the “what” question, at a cost in computer time. The “how fast”
question has been addressed by simulation tools in which time delays are
computed more accurately, such as by using RC circuit models in switch
level simulators. These have proved essential tools in getting full custom VLSI
designs to operate correctly the first time they are fabricated. Now with FPGAs
the computation of wire path delays can be complicated because the paths are
active in the sense that routing uses transistor switches and multiplexors. It
is infeasible to compute the behavior of FPGAs at switch level. Delays through
FPGA cells can, however, be modeled by a finite set of constants and path-delay
computations built into timing estimators. Since the performance of a circuit
is usually determined by a single critical path, estimator tools can replace timing
analysis.
Figure 4–4. Display driver
schematic.
Figure 4–5. VHDL for
display driver.
Our example is a purely
combinational circuit, and the design can be validated by applying the ten
legal input vectors and observing that the output vectors are consistent with
Table 4–2.
FPGA technology raises some
interesting questions on the relevance of validation tools. Simulation tools
have only gained users in recent times due to rising complexity in systems
design and difficulties in designing application-specific integrated circuits
(ASICs). Before simulation, systems were built on breadboards with standard
components and a rapid wiring technology (wrapping, Multiwire, etc). But FPGAs
can be used as instantaneous breadboards and synthesis programs create valid
designs algorithmically. The FPGA technology push is already creating more
interest in design methodologies. One can predict that areas like design
debugging will come under review now that equivalents to software debugging
techniques are available in hardware.
4.1.3 Tools
for Physical Design
Physical tools address the question
“how do I make this (structural) design fit physical reality while meeting
performance requirements?” All electronics technologies deliver finite spatial
resources for building functions and communications (wires). Resources are
especially tight with FPGAs, as the convenience of programmability is bought at
the cost of chip area for control store.
Conceptually the simplest tool,
and one that provides the essential handle on reality, is the graphical
editor. For FPGAs it is most likely to be a symbolic editor since it
is desirable to abstract away the underlying details of the silicon. The
figures in this book mostly show symbolic artwork of two FPGA families.
The physical design process can
be greatly assisted by automating the generation of random and regular logic. Block
generators for regular structures such as read-only memories and
programmable logic arrays are normally part of a software supplier’s package.
Generators can also be custom built by engineers using ordinary programming
languages. For random logic, placement-and-routing routines can be used
to build both random logic blocks and to assemble blocks at higher levels.
The total spatial demand of a
design includes a component for function units and a component for wires. It is
important to know early on if the spatial demand of a design can be met by the
spatial capacity of a particular FPGA. Estimator and fitter
programs assist in this task by computing function and wire demand for a
particular design for comparison with members of a standard part family.
The result of running standard
physical design software on the display driver example is shown later in
Figure 4–13. It shows a logic cell array (LCA)
implementation and two configurable array logic (CAL) implementations: one
using a ROM generator and synthesis program and the other handcrafted logic. It
exposes the eternal verity that humans can outperform algorithms, in this case
by a factor of 2, provided the design is tractable and there is sufficient
(human) design time.
It is likely the small example
we have been using is only part of a bigger design. In fact it was taken from a
VLSI class exercise in which the design specification is as given in
Section 4.4. In this case a key physical design
activity is
floor planning, in which the gross disposition of units in
the design and a wiring strategy for the design are defined.
Editors,
generators, and place-and-route programs can all assist the floor planning
phase.
Precooked designs are also a
useful source of tested designs with proven layouts. These are usually found in
supplier- or user-distributed libraries
[Newk83].
4.2 THE
FPGA DESIGN DICHOTOMY
One of the interesting properties of
FPGAs is that they merge what up until now have been two diverging families of
electronic products: programmable logic devices, notably PALs, and ASICs,
notably gate arrays and cell-based ICs. Each strand imposed a different
implementation style on the engineer, each came with its preferred design
process flow, and each came with its preferred toolset. The following sections
set out to show explicitly how FPGAs can be designed either from an ASIC or PLD
perspective.
Parenthetically,
it is too simple to suggest that only two design methodologies and toolsets are
important. In reality methodologies should be designed and toolsets chosen to
match the end FPGA application. For example, one could classify the chief
applications areas of programmable logic as: ASIC, ASIC emulation, and
algorithm implementation/coprocessing, in which case the following observations
would be relevant to method and toolset.
ASIC
Simple ASIC: A PAL design
methodology that places emphasis on tools for capturing a behavioral
description, optimizing logic equations and fitting the design to a member of a
standard part catalog.
Complex ASIC: ASIC design
places emphasis on both high-functionality tools for tasks like synthesis and
automatic place-and-route, and low-level tools for complete design control and
low-level optimization. More details are contained in the following sections.
ASIC Prototyping: The
assumption here is that the real implementation is probably a gate array or
cell-base IC (CBIC). So emphasis is in transforming a schematic to a netlist in
the most painless way possible. Automatic tools for physical design are key.
There is a desire for technology independence, but the preservation of
gate-level equivalent circuits may be a better design goal.
Algorithm Implementation: Algorithm
implementations usually exhibit some “natural” structure: cellular automata,
systolic circuits, self-timed micropipelines, pipelined coprocessors, dedicated
datapaths, and so forth. Emphasis is on the very efficient design of a basic
unit using low-level tools like symbolic editors and structure compilers.
4.3 DESIGN
PROCESS FLOW: THE PROGRAMMABLE LOGIC DEVICE ROUTE
A typical programmable logic device
(PLD) design process flow is shown in
Figure 4–6. The starting
specification
might be informal and hand drafted in anything from an HDL to a collection of
Boolean equations.
Design capture moves the design into the CAD
environment and requires the engineer to restate the creation for machine
consumption. This might be preparing a file in a preferred notation or marking
entries in a table.
Synthesis and optimization uses algorithms to
manipulate the logic design to improve it by exploiting don’t care states to
minimize the number of gates used.
Function verification may be a
unit-delay simulator to generate circuit outputs, or may amount to a manual
inspection of truth table data.
Device fitting matches logic/gate demand
and input/output (I/O) demand to part family members. Finally,
physical
design produces manufacturing data, a binary stream, for programming
specific devices. This must be achieved by generating a layout of the required
circuit in the chosen FPGA cell and wire scheme. It may amount to running a
simple logic block generator or it may be placing and routing random logic
using manual and automatic software tools.

Figure 4–6. PLD design
process flow.
4.3.1 Conceptual
Design of Display Driver
In the case of a CAL design the
specification is given in
Table 4–2. The minimization of this table using
ESPRESSO
[Brayton84] is shown in
Table 4–3. Now this is a standard sum-of-products
form that we can expect to implement within an array of cells that allows a
two-level logic structure to be built.
In the case of the LCA
implementation, because there is no “natural” form for implementing a two-level
logic structure, designs must be created as fully instantiated (flat) netlists.
For the display driver design specified in the PALASM2 of
Figure 4–3, a netlist must be optimized by
proprietary tools to accommodate implementation in configurable logic blocks
(CLBs) and the result merged with a top-level schematic to create the complete
design.
4.3.2 Design
Verification of Display Driver
In the case of the CAL design, since
the logic was synthesized there is no formal verification step other than
informal inspection of the truth tables.
In the case of the LCA design,
the flat netlist of logic primitives can be exercised with a logic simulator.
The result of this for a
test pattern of the ten digits is shown in
Figure 4–7. Readers can manually construct the
digits from the output to confirm the correct functions are being computed.
4.3.3 Physical
Design of Display Driver
In the case of the LCA implementation,
the result of applying placement and routing algorithms to the merged netlist
is shown in
Figure 4–23.
In the case of the CAL
implementation, physical design can be automatic, as in the synthesized ROM
logic block of
Figure 4–21, or physical design can be place and
route (manual or automatic) from a suitable gate-level netlist. Using the
gate-level schematic of
Figure 4–4 yields the manual design shown in
Figure 4–22. The synthesized ROM is further
described in
Section 4.5.1. It is interesting to compare the
quality of the logic synthesis with that of a manual implementation generated
with software design tools. The configurable logic ROM implementation requires
an 11 (4 inputs plus 7 outputs)-by-8 (product terms) array of cells compared
with an ll-by-4 array when implemented by hand. The following points are worth
noting:
Figure 4–7. Result of
simulating display driver.
- Flexibility. The
greatest advantage of the human-generated implementation is the way the
layout of the logic unit has been optimized to fit in with the chip
pin-out requirements and the counter design. Although there is a structure
to the layout (note that input variables are routed horizontally across
the array and outputs are collected using vertical wires), it is specific
to this particular example.
- Variable
Ordering.
In the automatically-generated array the order of the input variables in
the cascade of gates is fixed. Only the function performed by gates in the
cascade can be changed. The human implementation achieves a much better
factorization of the logic equations by changing the order of variables in
the gate cascades and using trees rather than simple cascades of gates.
This can only be achieved by having a special routing plan for each function
implemented.
- Design
Time.
Although the automatic implementation is much less efficient, it only took
about 10 minutes. The human-generated implementation took several days.
- Design
Size.
This example approaches the limit of the size of circuit which may be
designed efficiently by a person, and at this level of complexity, human
design may surpass automatic design. But for the most part circuit
optimization can be left to algorithmic methods.
4.4 DESIGN
PROCESS FLOW: THE APPLICATION-SPECIFIC INTEGRATED CIRCUIT ROUTE
There are many sources of ASIC design
process flows. VLSI design methodologies
[Mead80],
[Weste93] and ASIC manufacturers
[Naish88] are good sources. The former place
greater emphasis on layout issues, such as wiring management, to achieve
optimal physical designs, while the latter largely rely on structural design to
manage the whole process flow. A generic model for ASIC process flow is shown
in
Figure 4–8. Both the Gajski-Kuhn and more
traditional forms are shown. This indicates the refinement of a
specification
to a
structural design before entering design validation and physical
design processes. In reality the behavioral and structural descriptions are
built by stepwise refinement of the design. A typical ASIC design process flow,
represented by paths in the Gajski-Kuhn diagram, shows the three design
descriptions being built and the grain of the design unit decreasing. Thus a
starting behavioral
specification posits a
structural design.
This could be a composition of interconnected function units. This, in turn,
could be stepwise refined by expanding to a structural design of simple
elements, a gate-level netlist, or synthesizing a two-level logic block.


Figure 4–8. ASIC design
process flow.
To illustrate the flow let us
return to the display driver example. In fact, the 7-segment display driver was
part of a larger timer design exercise for a VLSI course. It had the
specification: Design a simple stopwatch to count in tenths of a second to one
minute and display the current time on three 7-segment displays (tenths,
seconds, and tens of seconds). The watch is controlled by three signals: INIT
clears the watch and puts it in the “stop” state, SS start/stop is a high-going
edge to start the watch from the stop state (a high-going edge in the start
state puts the watch in the stop state), CLOCK, a 10-Hz signal.
4.4.1 Conceptual
Design of Stopwatch
The 7-segment decoders provide a good
example of “random” combinational logic, while the counters provide a good
example of classic sequential logic. This design uses three separate units for
the three displays although the design complexity and area could be reduced by
implementing it as a single-state machine with multiplexed displays (since the
large 7-segment decoder logic would not need to be duplicated). This is
necessary to comply with the design specification given.
The Counter The
counter is built from four toggle flip-flops (
Figure 4–9). The basic 4-bit ripple counter is
converted to a decade counter by a gate that sets the clear line when the
counter gets to ten. The output of this gate is also used as the clock for the
succeeding counter. The counter can also be cleared by the user’s INIT signal.
Providing the clear capability is the only real problem in the design of the
toggle flip-flop (the basic D latches have only clock and D inputs). The clear
is provided by extra logic gates that force Os onto the D inputs and 1s onto
the clock inputs. A basic master-slave flip-flop can be built with only two D
latch cells, whereas this clearable implementation requires six cells. The
layout is shown in
Figure 4–10.
Figure 4–9. Toggle
flip-flop design.
The Decoder The
decoder takes advantage of the ability to produce any function of two Boolean
variables within one cell and uses three levels of logic rather than the
two-level logic normally used to implement such functions. Its schematic
description is given in
Figure 4–4 and physical design in
Figure 4–22 later.
The Control Logic The
controller function (at the bottom left of
Figure 4–11) is implemented using a toggle
flip-flop. The design is the same as those within the counters. The toggle
flip-flop is clocked by the start-stop input and its output determines whether
the counter should be stopped or run freely. The initialize signal clears the
control flip-flop and stops the counter. The counters are stopped by ANDing the
10-Hz clock with the output of the control flipflop: thus when the output of
the control flipflop is 0, the counters clock inputs are held low, and when it
is 1 the counters receive the 10-Hz clock input.
Figure 4–10. Counter
design.
Figure 4–11. Full Stopwatch
design.
Figure 4–12. Stopwatch
floorplan.
4.4.2 Design
Verification of Stopwatch
See Problem 3.
4.4.3 Physical
Design of Stopwatch
The floorplan of the full watch
circuit is given below as
Figure 4–12 and the layout in
Figure 4–11. The floorplan is based on using three
sides of the design to make connections to each of the displays accessible and
the fourth side to get the control signals into the chip. Note that the
floorplan requires simple transformations, rotations, and mirroring of the
basic unit.
4.5 LIBRARIES
AND DESIGN IDIOMS
In a sense design is idiomatic.
Engineers can express designs in modes particular to a set of components at a
specific level of design abstraction, for example, register transfer elements,
or components particular to an implementation style for example, small-scale
integration (SSI), MSI, and LSI TTL
[TTL88]. If one adopts a bottom-up view of the
world, then large designs are viewed as made up from aggregations of elementary
components, usually gates. Since electronic logic by and large evolved from TTL
elements, designs are perceived as compositions of TTL primitives. History has
created a data base of collective design experience. This data base may be
mined to create new designs from old experience, provided a set of primitive
components exists in the new implementation style. This view has led the ASIC
vendors to reproduce TTL libraries for customers’ use in designing (see
Table 4–4). Alternatively, if one adopts a
top-down view of the world, large designs are composed from generic high-level
elements, such as counters, ALUs, and register files, whose specific features
are defined in the design refinement process. This view of designing has led
the ASIC suppliers to provide parameterized register-transfer (RT) and
processor-memory switch (PMS) level component libraries,
Table 4–4.

These hard and soft libraries
are equally valid ways of collecting design experience and making it available
to practicing engineers in tried and tested forms. Hard libraries try to
maintain historical certainty in the encapsulation and functions of their
elements. In a sense, they are fossilized design fragments that may limit the
optimality of complete designs. Soft libraries can provide “made to measure”
components for optimal designs at the expense of variations in performance for
particular instantiations.
4.5.1 Parameterized
Libraries
It is often very useful to think of
library components as elements “sized” to a set of parameters: an n
input gate, an n word by m bit stack, and so forth. In building a
circuit the parameters are replaced by integer constants to suit the
application. A simple way of satisfying this requirement would be to fill a
library with all useful instantiations of a parameterized module and select a
particular one by indexing from the parameter. This approach allows for more
precise characterization of library elements at the expense of more storage. An
alternative approach is to use the parameters in a program to generate
the precise instance required. Two examples of this approach are described in
the following subsections.
Parameterized Modules The
requirement is to build a count “up-to-
n” circuit. A generic counter and
comparator, and constant generator, could be used to fit the requirement. The
alternative approach would be to compose a counter from stages, each of which
could test for a 0 or 1 depending on the position of these binary digits in the
constant. By adding comparator gates, see
Figure 4–13, to a basic toggle register we have
the elements for building a count up-to-
n circuit. The power of a
programming language can be harnessed to assemble such a part. We need to build
a vector of counter stages, each of which is conditionally defined. The
iteration and conditional selection features of a programming language are
well-suited to this task, provided there is a library of routines for
describing and instantiating cells. The fragment of C code shown in
Figure 4–14 shows this for assembling the
“onestage” and “zerostage” of
Figure 4–13. With
upto = 5, the
count-to-five circuit of
Figure 4–15 would be generated.
Block Generators: The
Configurable Logic ROM Generator With cellular FPGAs
there is likely to be a simple way of implementing a two-level structure. In
the case of CAL it is a configurable logic ROM. We will describe how it works
by first discussing a simpler but less efficient scheme.
Simplified Version This
version consists of an
n-bit decoder, an “AND” plane, producing 2
n-1
minterms feeding a special “OR” plane which uses two gate functions. As shown
in
Figure 4–16, the Algotronix CAL cell has four
inputs, one per side. Any two can be selected as XI, X2 for the evaluation of
an arbitrary Boolean function. The simplified CAL-ROM layout is shown in
Figure 4–17. If the row is selected, the cell
function depends on whether we require 0 or 1 output for this particular bit.
On the other hand, if the row is not selected, we simply pass through the input
received from the cell below, to take care of the case where the selected row
is below. If the selected row is above, the output of this cell is of no
consequence.
Figure 4–18 gives the CAL cell configurations.
Compact Version The
height of the array can be cut in half, and the decoder width reduced by one
cell. The last input variable is introduced at the bottom of each OR-plane
column, as shown in
Figure 4–19, and each cell in the OR-plane
computes a function of this variable and one of the minterms. If the row is
selected, the input from below must be AO. If the row is not selected, it may
either be below or above the selected row. In either case, it simply passes on
the input received from below—either A0 or the output of the selected row. The
cell function chosen depends on the value desired for A0 = 0 and A0 = 1, as
shown in
Table 4–5 and
Figure 4–20. The program
lisa automatically
generates this arrangement for a multiple-output function given an arbitrary
truth table.
Figure 4–13. Stages for
count-to-n circuit.
Figure 4–14. CAL operation.
Figure 4–21 shows the resulting layout of the CAL
cell array, in which the 4 inputs appear at the lower left hand edge, q3, q2,
q1, q0 and the outputs a,b,..., g at the upper edge.
Figure 4–22 is a manually-composed alternative,
with the inputs at the left and outputs at the right.
Figure 4–23 is a layout for a Xilinx XC3020 design
using the logic schematic given in
Figure 4–4 as input.
Silicon Compilation The
examples in this section of parameterized modules and generated blocks have
shown physical synthesis from high level descriptions. The term “silicon
compilation”
[Gray79], has been applied to this process. In the
case of the counter modules, the start point was a number of schematics for
count cells, and a C program was designed to compose the cells to form the
function. Because the start point for this process was a structural
description, the C program and (software) library functions represent a
structure
compiler.
In the case of ROM block
generator, the start point was a truth table, so the process was behavior
compilation and the synthesis software represents a behavior compiler.
Figure 4–15. Count-to-five
circuit.
Figure 4–16. CAL cell.
Note: the output is a function of the West (× 1) and South (×2) inputs.
Figure 4–17. Simplified
CAL-ROM layout.
Figure 4–18. CAL cell
configuration.
Figure 4–19. Compact
CAL-ROM layout.
Figure 4–20. CAL cell
options.
Both examples show the power of
silicon compilation techniques in generating substantial design fragments
quickly and with guaranteed structural integrity.
Figure 4–21. Physical
designs for the display driver: ROM-based CAL design.
4.6 PLACEMENT,
ROUTING, AND WIREABILITY
An eternal requirement in CAD tool
provision is for automatic place and route, preferably with 100% guaranteed
success and with a short run time. Unfortunately, placement and routing takes
place within the context of a real design and physical reality imposed by one or
more FPGAs, the implementation medium. Any design contains a demand for wires
with its point-to-point connections and bus structures. Since the FPGA contains
a finite number of wires, all FPGA architectures have a defined wiring
capacity. When there are gross discrepancies between the wiring demand of a
particular design and the wiring capacity of the target FPGA, it is likely to
be difficult to discover an implementation by any method including advanced
placement and routing algorithms. It is worth trying to understand the
relationship between wiring capacity and demand so that better engineering
decisions can be made about the suitability of a particular FPGA for a
particular design.

Figure 4–22. Physical
designs for the display driver: manual CAL design.
4.6.1 Rent’s
Rule and Package Pin-outs
Rent’s rule was originally
“discovered" from examining packages of logic modules
[Russo71]. It attempts to answer the
question, “How many connections (
n) are required to a structure holding
a number of components (
N) each of which has a number of connections (
m)?”
(see
Figure 4–24). The relationship can be
stated as
n ≈
m *
N(l-p), where
p
is Rent’s coefficient (≈0.5). It has an intuitive explanation if one imagines a
square array of components on a board. Cutting the board in half, creating two
edge connectors, would expose
m wires. The rule can be applied as a
“sanity check” on components that deliver random logic, like FPGAs, which are
made of
N logic cells with
m pins contained in packages of
n
pins. To make the most use of an FPGA while implementing random logic, the
ratio of user I/O package pins to connections to the logic cell should be
according to Rent. This exercise is left to the reader to be applied to the
commercial offerings at any point.

Figure 4–23. Physical
designs for the display driver: LCA design.
4.6.2 Rent’s
Rule and Wireability
Heller et al.
[Heller78] were the first to attempt an
analysis of wiring demand, in this case for logic designs in the context of
gate array “images.” They addressed questions such as: What characterizes
useful gate array architectures? How big should wiring channels be? What is the
average interconnection length of wires? What is the distribution and number of
interconnections? Simple one- and two-dimensional models (see
Figure 4–25) can be used. This shows three
terminal logic elements communicating with a wiring channel of fixed capacity
(the capacity in the two-dimensional case is the sum of the horizontal and
vertical wiring channels). By using Rent’s rule to compute average wire length
and making an assumption on the distribution of wires, it is possible to
estimate a channel capacity that will allow the interconnection of a given
number of logic elements. This is shown in
Figure 4–26. It shows that even for
relatively low gate counts, the ideal channel capacity is high, but as the gate
count grows logarithmically, the channel capacity grows linearly. The analysis
also covers variation for
m terminal logic elements. The result
indicates that to help the wireability of a design, the FPGA architecture, or
structures built from it in the case of channelless arrays, should support
channel capacities corresponding to gate count as in
Figure 4–26.

Figure 4–24. Two levels of
physical hierarchy.
Figure 4–25. Idealized
wiring models.
Figure 4–26. Variation in
wire demand with gate count.
4.6.3 Partitioning
Designs within and across Chips
Partitioning is important in three
areas:
- Partitioning
the resources within a single FPGA to support multiple designs
- Partitioning
a design into subsystems for placement onto regions of an FPGA
- Partitioning
a very large design across more than a single FPGA part
An example of the first case is shown
in
Figure 4–27. In this case, each of the
subsystems is self-contained and can be designed in isolation. There are at
least two important design decisions: can the subsystems be fitted onto the
chip? and does the pin-out make sense at the board level? It is likely that
there is more than one choice of implementation of each subsystem, and that in
the
parcel packing problem, in laying out the chip, the modules may have
alternative shapes. This degree of freedom can be important in making feasible
designs. The second question can only be answered in the context of the board
design and involves matching the wire demand of the chip pin-out to the wire
capacity of the board (defined from the copper dimension design rules and
number of interconnect layers).
In the second case the need for
partitioning comes from a requirement to divide a large design into subunits
for implementation, the traditional divide and conquer approach to engineering
problems.
Figure 4–27. Multiple
designs on a chip.
PROBLEMS
1. Find a simulator and simulate
the display driver design from the logic.
2. Verify
Table 4–2 as a correct behavioral
description.
3. Verify the same logic block by
developing expressions for the outputs evaluating these expressions for the ten
binary constant inputs.
4. Simulate the whole design of the
stopwatch.
5. Comment on the overpinning or
underpinning of some commercial FPGA parts.
6. Describe a wiring strategy for
building random logic within a cellular FPGA consistent with wireability rules.
CHAPTER 5
CASE STUDIES
The
purpose of this chapter is to:
- Illustrate the stages in
transforming a problem definition into a working solution
- Provide illustrations of
typical design tools
- Show the usefulness of
hierarchy
We
have deliberately chosen elementary examples, which for the most part only use
a small portion of a field-programmable gate array (FPGA) chip, apart from the
final example of the videostore controller. The problems have been carried out
with Xilinx and Algotronix FPGAs, using CAD tools obtained from these companies
and ViewLogic Inc. Since CAD software is regularly improved, and command
sequences change, any detailed information on particular CAD tools would
probably be out of date by the time this book is published. We recommend that
you obtain the latest editions of data books, user guides, and so forth, from
the companies or their local distributors. At the end of the chapter there are
suggestions for projects you might like to try for yourself.
The
Xilinx examples have been developed for a generally available demonstration
board, which is shown in Figure 5–1. It has eight switches for input, eight individual
light-emitting diode (LED) displays for output, and a 7-segment numerical LED
display. Some of the examples have been devised to fit this restricted set of
circumstances.
Figure
5–1. Xilinx demonstration board.
Photograph courtesy of Xilinx, Inc. © Xilinx, Inc. 1991. All rights reserved.
(Photograph by P. Crockett)
5.1 COMBINATIONAL
CIRCUITS
5.1.1 Parallel
Adder Cell
The simplest form of parallel adder is
a
ripple adder, which consists of a cascade of 1-bit full adder cells.
Each cell has inputs
A, B along with carry input
C. It produces
outputs SUM and CARRY, determined by the Boolean equations for a full adder,
corresponding to the truth table shown in
Table 5–1.
SUM = A... + Ā.B. + Ā..C
+ A.B.C
CARRY = A.B + A.C
+ B.C
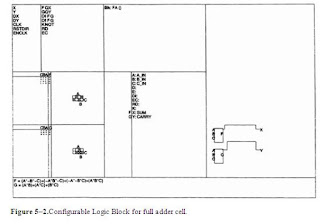
Xilinx Implementation The
equations may be entered directly as the
F and
G outputs of a
Xilinx 3000 series Configurable Logic Block (CLB), since each output can be an
arbitrary function of up to four variables chosen from a total of five inputs.
Since the functions are implemented by look-up tables, there is no advantage in
manipulating the equations further. For such a simple case it is easy to enter
the details directly on the CLB array with the editor
XACT. Figure 5–2 shows the block concerned, while
Figure 5–3 shows the routing to input and output
pads. The routing was determined by
XACT after each net had been given
as a list of pins. The configuration of each input or output block can also be
specified with
XACT, in this case direct inputs and outputs. The design
details were saved to a file to be used as input in generating a configuration
bit-stream file for downloading to the chip itself.

Alternatively, a schematic
diagram for the adder may be entered as a logic circuit, as shown in
Figure 5–4, which was prepared with the editor
ViewDraw.
This was used to generate a netlist, that is, a file specifying the logic
elements used and how they are interconnected. The netlist can be used for
functional simulation with a simulator such as
ViewSim, as shown in
Figure 5–5. Since the design has not at this stage
been mapped to an actual FPGA, this is only a functional simulation, and there
is no useful timing information. Translation to an actual Xilinx configuration
will be deferred until we have a more substantial example.
Algotronix Implementation Since
the configurable array logic (CAL) block functions have two inputs, the
equations need to be reexpressed:
SUM = (A ⊕ B) ⊕ C
CARRY = (A.B) + ((A
+ B).C)
The 1-bit adder can be laid out in a
block of 3 × 3 CAL cells as shown in
Figure 5–6. The graphical editor
clare was
used for this purpose, and allows the user to specify the function of each cell
and routing to and through it. The lower left cell holds the datum for the
block. Note that the cell is arranged so it can be cascaded vertically, with
the least-significant bit at the bottom.
5.1.2 Parallel
Adder
We can assemble a ripple-carry adder
by simply cascading the full adder. We use a 4-bit example.
Figure 5–2.Configurable
Logic Block for full adder cell.
Figure 5–3. CLB array for
full adder cell (XACT).
Xilinx Implementation Figure 5–7 shows a schematic prepared with the
schematic capture program
ViewDraw. There are four instances of the full
adder cell referred to in
Section 5.1.1. To use it with the demonstration
board, we need a top-level schematic, which is shown in
Figure 5–8. This shows the specific input and
output pads, which are connected to the dual-in-line switches and LEDs,
respectively. Again, the design may be simulated at this stage, that is, at a
functional level, and
Figure 5–9 shows results of applying a set of
input vectors VA, VB resulting in the output vector VSUM. The process of
converting the design into an FPGA implementation requires the following steps:
Figure 5–4. Schematic for
full adder cell (ViewDraw).
- Derive
a netlist from the schematic editor. This specifies the circuit in logic
detail, still in terms of idealized elements.
- Map
the logic circuit to the particular technology of the Xilinx 3000 series
CLBs, and input/output blocks (IOBs). This is a complex process, since
each CLB can generate two output signals, and the aim is to reduce the
total number of CLBs required. At the same time, some simplifications can
be made, for example, redundant logic can be removed.
- Placement,
which starts from a random assignment of CLBs to positions in the logic
array. For this design, the IOB positions are predetermined by the
demonstration board. The initial placement is evaluated in terms of
estimated wire length, based on the connection points of each net. The
placement is improved with an iterative process known as simulated
annealing, which moves CLBs to reduce the estimated wire length.
- Routing.
Each net is connected according to the netlist, and uses the variety of
available routing resources: direct connections from a CLB to its
immediate neighbor, connections via switch-matrices, and long horizontal
or vertical connections. This process results in a file containing details
of the placement and routing.

Figure 5–5. Simulation of
full adder cell (ViewSim)
Figure 5–6. Configurable
array logic for full adder
- Bit-stream
generation. The bit stream specifies the “program” for the FPGA, that is,
the memory bits which control the function and internal connections of
each CLB, the settings of all interconnect switches, and the mode of
operation of each IOB.
The bit stream can be downloaded to
the demonstration board, and the design checked with switches and lights. Later
we will discuss a more systematic way of testing using random patterns.
Algotronix Implementation The
graphical editor
clare was used to create four instances, as shown in
Figure 5–10. Note that the cells cascade by
abutment. The design was placed on the Algotronix CHS2×4 board described in
Chapter 6, and was positioned in the northwest comer
so that signals could be applied and monitored easily.
5.2 SEQUENTIAL
CIRCUITS
5.2.1 Decade
Counter
This design was implemented for a
Xilinx 3020 FPGA with the aid of the ViewDraw schematic entry program,
the ViewSim simulator, and Xilinx software for CLB mapping, placement,
routing, and so on. The design illustrates alternative ways of creating a
decade counter:
Figure 5–7. Schematic for
ripple adder.
Figure 5–8. Top-level
schematic for ripple adder.
Figure 5–9. Simulation for
ripple adder.
Figure 5–10. CAL layout for
ripple adder.
- Using
a macro element for a synchronous decade counter functionally equivalent
to the 74160 TTL component
- As
a collection of gates and flip-flops
- By
direct entry to CLBs
Figure 5–11 shows the top-level schematic.
The demonstration board has an
RC controlled oscillator based on a
single configurable logic block. The GOSC macro, shown in the lower left of the
figure, produces a clock that runs at approximately 100 Hz when connected to
external
R and
C components through pins 12 and 14. Another pin is
connected to a dual in-line package switch that determines if counting takes
place, or otherwise holds the counters clear, depending on the signal COUNT_EN.
The oscillator is connected to the global clock GCLOCK, which in turn
increments the least-significant decade counter.
Figure 5–12 shows the schematic diagram for
the 74160 synchronous counter.
Figure 5–13 shows an encoded state machine
design. The next state (N) variables are determined from the present state (P)
variables.
Figure 5–14 shows the state machine for the
decade counter.
Figures 5–15 and
5–16 show the basis for the design, which
takes advantage of unassigned states that will of course never be entered, that
is, decimal 10-15, and assigns 0 or 1 depending on the resulting simplification
in the Boolean equations. For example, in deriving the least-significant bit N
0
of the next state, the box corresponding to present state , that is, “12”
(decimal) is assigned to 1 to allow the whole column to be taken, and later
combined with the right-hand column as
0. The fifth D flip-flop is
used to delay the carry-out following state “9” until the next count pulse
arrives.
Figure 5–17 shows how the CLBs may be set
up directly by the user, that is, assigning their mode and Boolean equations to
be implemented. Note that the three alternative methods are shown for
illustrative purposes, and that in practice the 74160 macro method would be
preferred by most users.
The schematic information was
used to generate a netlist for use by Xilinx software, which first mapped the
logic to CLBs, and then determined a good placement on the 8 × 8 CLB array. The
routing was completed automatically, and the CLB array layout is shown in
Figure 5–18. The
RC oscillator CLB
is at site BA in the upper left. Note that after buffering by the clock buffer
it drives two vertical clock lines in the first two columns. Some connections
between adjacent CLBs are made by direct connection, which is fast, while
others pass through the much slower switch matrices, revealed by the sloping
routing. Each decade uses four CLBs.
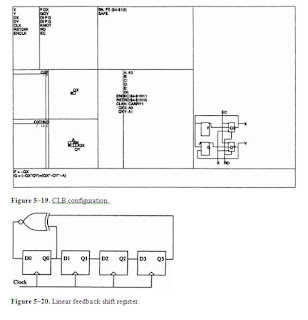
Figure 5–19 shows the settings of a
particular CLB at location FE—this corresponds to the two least-significant
flip-flops at the left-hand side. Interestingly, the mapping process has
swapped the roles of the two outputs, presumably to reduce interconnection
delay, as can be seen by comparing the figures. The configuration detail shows
that both of the edge-triggered D flip-flops are clocked on a rising clock edge
(K), provided the clock is enabled (EC). The reset-direct (RD) signal is used
to hold the counters clear.

Figure 5–11. Top-level
schematic for 3-decade counter.
Figure 5–12. Macro cell for
74160 decade counter.
Figure 5–13. State machine
for decade counter.
Figure 5–14. State sequence
for decade counter.
5.3 PSEUDORANDOM
NUMBER GENERATION
Random numbers can be very useful in
simulation and testing digital circuits. Here we will use these numbers in
testing the parallel adder described earlier. The term
pseudorandom is
used because the process is in fact completely predictable. The linear feedback
shift register (LFSR) method is a particularly simple one, which can generate a
sequence of length 2
n – 1 for a register
n bits long,
provided it has the correct feedback connections.
Figure 5–20 shows a 4-bit LFSR that can generate a
sequence of length 15, not including the all-Is state, which is a
lock-up
state—once entered, the register will stay in this state indefinitely.
Table 5–2 shows the feedback connections to
produce a maximal length sequence for various register lengths.
5.4 RANDOM
TESTING
For large systems, random testing is
often a practical alternative to exhaustive, or case-by-case testing, and may
be built into integrated circuits and systems.
Figure 5–15. Equations for
state machine: state encoding for decade counter, less-significant bits.
Figure 5–16. Equations for
state machine: state encoding for decade counter more-significant bits.
Figure 5–17. CLB entries
for decade counter.
Figure 5–18. Configurable
logic block array for 3-decade counter.
Input patterns may be readily
generated with the LFSR method just described. Signature analysis is a
technique for compressing the resulting output patterns into a short word whose
final value indicates success or failure. While compression inevitably could
allow some circuit failures to produce an identical signature, the risk is
usually small.
We will take the 4-bit ripple
adder described in
Figure 5–4.
Figure 5–21 shows the top-level schematic.
Since there are eight input bits, along with carry-in, we will use a 9-bit
pseudorandom number generator. To compress the four sum bits and the carry-out
into 4 bits to be displayed on the demonstration board LEDs, we use a 4-bit
signature analyzer.
Figure 5–19. CLB
configuration.
Figure 5–20. Linear
feedback shift register.
5.4.1 Signature
Analyzer
The signature analyzer is an
adaptation of the LFSR. At every clock cycle, a set of outputs from the ripple
adder is loaded in parallel to an LFSR, with the feedback connections given
earlier. These are XORed with the previous register contents as shown in
Figure 5–22.
TABLE 5-2. LFSR Connections for
Pseudorandom Sequence Generation
Register
Length
|
Feedback
Connections
|
2
|
0,1
|
3
|
0,2
|
4
|
0,3
|
5
|
1,4
|
6
|
0,5
|
7
|
2,6
|
8
|
1,2,3,7
|
9
|
3,8
|
Figure 5–21. Top-level
schematic of a parallel adder.
Figure 5–22. Signature
analyzer.
Figure 5–23. State diagram
5.4.2 State
Machine
As discussed in
Chapter 2, state machines can be
implemented in different ways. Encoded state machines may minimize the storage
required, but at the expense of decoding logic, reducing speed. Here we use the
one-hot method, that is, one bit per state. The four states are as follows:
- Initial
state: wait for switch to be pressed
- Accumulate
signature from four output bits in signature analyzer
- Accumulate
carry-out bit in signature analyzer
- Display
4-bit signature on LEDs
Figure 5–23 shows the state diagram and
Figure 5–24 shows the schematic. Note that
State0 has inverting logic on both input and output, so that it automatically
goes high when the FPGA is powered-up. Also, the State3 output is used to reset
states 1 and 2 in the unlikely event of a logic state error, for example, if
either bit was simultaneously asserted with State3.
5.5 SYSTOLIC
SORTER*
This example is included to suggest
that FPGAs may provide novel ways of solving well-known problems. Sorting is
required in many computer applications, particularly commercial ones. Here we
look at a high-speed sorter, but one confined to miniscule amounts of data. It
is described as systolic because it uses a repetitive block structure,
and has a regular data flow. In general, each item to be sorted consists of a
number of fields, of which one is selected as a key, on which to sort.
For simplicity we regard the key as a nonnegative integer, and assume that we
wish to sort items in ascending order of their keys. For simplicity, we
concentrate on sorting the keys.
Figure 5–24. Schematic for
state machine.
Knuth
[Knuth73] distinguishes some basic sorting
methods:
Sort by insertion: Find the
correct place to insert an item in an already-ordered list
Sort by exchange: Consider
pairs of keys, and swap them if out of order
Sort by enumeration: Find the
smallest (or largest) key and remove the item to a new list. Repeat until the
original list is empty.
The scheme described here is a
combination of the first two methods. We assume that the items to be sorted
arrive individually, so it makes sense to keep previous arrivals in order—we
choose ascending. Borrowing a technique from full-custom VLSI design, we make
up blocks of cells, and arrange for simple connections of data and control
signals. The overall floorplan is shown in
Figure 5–25. Each key is stored in a
vertical column of one-bit blocks, with the least-significant bit at the top,
and the most-significant bit adjacent to the control block at the bottom. New
keys arrive at the left-hand side, and will “ripple” to the right, as they are
compared with stored keys until they fall into the correct column. Each control
block, of which there is one per key, simply uses the result of the arithmetic
comparison made above:
if the stored key (S) is smaller
than the one to its left (L), key L is passed to the cell on the right, i.e.
bypassing S. otherwise, L must be stored in place of S, and S passed to the right.
Figure 5–26 shows the data flow for the
comparator cell, as implemented in Algotronix CAL logic. When all the keys have
been submitted, the sorted list is returned by a series of left shifts, that
is, so the smallest key emerges first.
Figure 5–25. Systolic
sorter.
Figure 5–26. Sorter
comparator cell—data flow.
In every column an arithmetic
comparison is made, commencing with the less–significant bit at the top of the
key. Each bit stage generates a signal “less,” which indicates that, based on
the series of bits so far, the stored key is less than the one to its left.
This result may change as the more significant bits are considered. The
comparator logic is illustrated in
Figure 5-27, and is described as follows:
Figure 5–27. Sorter
comparator cell. Comparison logic.
if the left-item bit and the
stored bit are equivalent, pass on the “less” result from the Is comparator
above. otherwise, if the left-item bit is a 1, set “less” to 1 or if a 0, then
set “less” to 0.
It is implemented in the 1-bit
comparator shown in
Figure 5–28.
The control block is shown in
Figure 5–29. Before sorting starts, the
CLRb signal sets all the D flip-flops to 1, and as keys appear, Os are
propagated through the control blocks. When the set of keys to be sorted has
been entered, the results are retrieved in an ascending order by issuing a set
of “read” instructions, which shift the contents of the control and key blocks
left.
Figure 5–30 shows an overall view of the
sorter.
5.6 MULTIPLIERS
Multiplier designs are a simple way of
studying different varieties of digital logic designs. It is possible to develop
different multiplier examples to study the varieties of design approaches and
implement these designs using FPGAs. In the following sections Xilinx 3000
implementations are assumed, but the approaches vary from fully automated to
handcrafted with corresponding gains in performance.
5.6.1 Parallel
Multipliers
The simplest of the multiplier designs
is a parallel-combinational logic multiplier. This multiplier produces a result
by adding the partial products of equal binary weight with the carries of the
lower binary weight. The design consists simply of AND, OR, XOR, and inverter
gates at the top-level schematic.
Schematic Entry Figure 5-31 is an example of a 4- × 4-bit
combinational logic multiplier. The design was created using ViewLogic
WorkView.
Using CAD tools, a logic design can be entered directly as a top-level
schematic, manually connecting gates together. To obtain more information about
creating a schematic design, refer to the current Xilinx and/or Viewlogic
WorkView
manuals.
Functional
Simulation It is always a good idea to check the
design functionality before actually continuing with the creation of the layout
file. The software used to create the schematic design provided support for a
functional simulation of the schematic circuit. Refer to
Figure 5–32.
Figure 5–28. Comparator.
CAL block.
Figure 5–29. Control: CAL
block.
Figure 5–30. Overall layout
of sorter.
Figure 5–31. 4- × 4-bit
combinational multiplier.
Figure 5–32. Waveform for
functional simulation.
File-conversion Process
In order to be able to create a Xilinx layout for the parallel multiplier, it
is necessary to follow a series of steps to convert the file to the correct
format. The file-conversion process consists of the following steps:
- Generate
a “wirelist” (net) file from the schematic level file
- Generate
a netlist file from the wirelist file
- Generate
a layout file using the automatic router
Speed Most
of the technology used today requires the use of high-speed circuits. The speed
performance of the Xilinx design will be affected by several factors: choice of
part being used, the arrangement of the programmed logic within the circuit,
and the efficiency of the layout itself.
XACT Design Entry It
is possible to enter a design directly by using
XACT (the Xilinx design editor).
This can be done by configuring the blocks directly, using logic expressions
instead of entering a schematic.
Figure 5–33 gives an example of the
multiplier as entered using
XACT.
5.6.2 Serial
Multiplier with Parallel Addition
Another example of a multiplier
circuit is a serial multiplier. The main difference between the parallel logic
multiplier and the serial multiplier is the introduction of memory and timing
in the design.
Schematic Entry Figure 5–34 is a schematic for a serial
parallel multiplier created using ViewLogic
WorkView.
The serial multiplier can be
processed as before to generate the Xilinx layout file.
Figure 5–35 shows the serial multiplier
layout configuration for a 3000 family Xilinx chip.
5.7 A
PARALLEL CONTROLLER DESIGN*
An outline of the design and
implementation of a video framestore design is presented that used the Petri
net method described in
Chapter 2, and is implemented on a Xilinx
LCA.
The function of the framestore
is to receive or transmit digital video data from a memory in a raster scan
format. Region of interest (ROI) is supported, allowing the reception and
transmission of frames of any size. Video data arrive on a 16-bit-wide bus
every 100 ns. A frame synchronization signal defines the start of a field of
data of 260 lines by 760 pixels. Each line starts with a horizontal
synchronization signal. The video controller has to deposit the data in a video
framestore in the correct order (interleaving two fields to create a full
frame) and to manage accesses to the memory. A second independent video channel
operates at the same time, but it must access a different block of memory. A
transputer is able to access both memory blocks while video operations are
being performed. At the end of a frame, the video channels may be required to
switch memory banks, and this must be handled by the controller.
Figure 5–33. XACT
view of the parallel multiplier.
The controller has a number of
registers containing its operating parameters, such as horizontal start and end
count, vertical start and end count, and start address in memory.
Figure 5–36 shows the datapath structure of
the controller design. It contains all the datapaths and a large Petri net
controller and has been implemented in a Xilinx 3090 FPGA.
Figure 5–34. Schematic for
the serial multiplier.
Figure 5–35. XACT
configuration for the serial multiplier.
5.7.1 Operation
of Part of the Petri Net Controller
The controller Petri net uses
inhibiting and enabling arcs and is made up of many small linked Petri nets. To
illustrate both the Petri net technique and its use in hardware design, a small
fragment of the controller is described.
Figure 5–37 shows the parts of the
controller associated with generating the horizontal synchronous output signal,
‘HsyncOut’, and with determining the position of active pixels within a line.
Consider that the circuit is initially idle, and is to be operated as a timing
master, with ‘HsyncOut’ connected back to the controller’s ‘Hsync’ input.
Although ‘Hsync’ is not directly used in this part of the circuit, its
assertion will cause the external pixel counter, ‘Hctr’ in
Figure 5–36, to be reset and thereafter to
count toward the register values ‘Hstart’ and ‘Hend’, so that the Petri net
inputs ‘HctrAtHstart’ and ‘HctrAtHend’ are asserted at the appropriate times.
Figure 5–36. Simplified
block diagram of the MAXbus controller.
An image transfer is initiated
when an “arming” transition fires in another part of the net, causing a token
to arrive in P3. This token is removed on the next clock cycle, so that the
arming signal is only one cycle wide. The arming signal enables transition T4,
so that on the next clock cycle T4 fires, removing the token in P4 and thereby
releasing the “done” output to indicate that the controller is running. The
arming signal also enables transition T1 so that on the next clock cycle the
token in P2 moves to place PI, asserting ‘HsyncOut’. Having no other associated
conditions, transition T2 will immediately fire on the following clock cycle,
returning the token to P2. ‘HsyncOut’ is thus one cycle wide.
As mentioned earlier, the
generation of the ‘HsyncOut’ signal causes the pixel counter to be cleared, and
to count toward ‘Hstart’ and ‘Hend’. When ‘Hctr’ reaches ‘Hstart’,
‘HctrAtHstart’ is asserted, T5 fires, and ‘Hblank’ becomes inactive. External
circuitry (the serial clock in
Figure 5–36) uses this signal, together
with a ‘Vblank’ signal generated elsewhere, to decide whether to clock active
data. Later, ‘HctrAtEnd’ is asserted and T6 fires, reenabling ‘Hblank’. The
assertion of ‘HctrAtHend’ also has the effect of firing transition T3, thereby
generating a further ‘Hsync’ output from place PI, to indicate the start of a
new line. The process continues until a token arrives at P4 indicating that the
sequence is done and this inhibits T3 from firing.
Figure 5–37. A small part
of the controller.
5.7.2 Characteristics
of the Design Technique
It can be seen that the small ‘Hblank’
circuit lies in a separate Petri net running in parallel with the rest of the
circuit. The introduction of parallelism in this conventional way is over and
above the parallelism that can be expressed within a Petri net. Parallelism is
used in the circuit both to have more than one task running at a time and
simply to express the design more easily. In the case of the ‘Hblank’ circuit,
this convenience allows the implementation to be a natural expression of the
definition of horizontal blanking, taking place from the end of one line to the
start of the next.
5.7.3 Implementation
on XC3090
The design was entered in schematic
form to the ViewLogic CAD system. Four designs have been produced: an 8-bit
design and a 16-bit design, each with and without ROI capability. These have
all been simulated using nominal delays for the logic cell array (LCA) circuit
components.
The full 16-bit design uses 83%
of the 320 CLBs and 86% of the 144 IOBs available. This design could not be
routed automatically on the tools available at the time (1991). An early effort
to cut down the design to 68% CLB usage also proved to be unroutable using
automatic tools. For comparison, an inoperable version with 50% CLB usage was
routed automatically. With smaller array parts, automatic routing was
successful at 80% CLB usage. However, it was clear that the place-and-route
strategies in the software could not cope satisfactorily with the larger
arrays.
These problems were overcome
using informal tools from Xilinx for routing a functional block at a time. This
system allows the designer to carry out floor planning, leaving space for
routing channels, which the automatic tools cannot do. The automatic router is
then run on the small blocks, where it manages to achieve a higher packing
density. Each iteration adds one functional block to the work already routed;
earlier routing is copied into the current iteration using the place-and-route
program’s (APR) guide option. Manual intervention, using the XACT LCA editor
program, is needed to tidy up the design at each stage. The newer design tools
from the manufacturer more adequately deal with these problems, as will be seen
shortly.
As a result of this experience the
following hints are offered for future users:
- Supplement
long lines by routing out on one side of the chip and back in the other
side.
- Bring
signals used in a number of places into the chip using multiple pins.
- Minimize
three state buffer usage as they reduce access to nearby CLBs.
- Minimize
use of the RD and CKEN pins on CLBs, as these cannot be swapped to other
locations in the way that, say, X and Y can, to make routing easier. The
exception is when driving a number of these pins from the same long line.
- When
using outer long lines to drive, the three state input to IOBs indicate
this to the router with a small piece of manual prerouting.
Two further problems were
encountered. The first arises when routing a block that has a pin that is to be
connected to another block that has yet to be routed. The pin can become buried
with no access path to it. To overcome this a dummy circuit is added, using XACT,
connecting to such pins, thereby forcing a route to be found before the current
iteration can be declared complete.
The second problem arises when
copying routing information from a previous iteration. During the routing
process CLB pins are swapped about to make routing easier. When copying routing
information from the previous iteration, the router attempts to repeat the pin
swaps already decided on. However, it occasionally fails, believing the pin
swaps to be illegal (which they sometimes are until other pin swaps have been
done first). This is tiresome, especially when it involves the loss of routing
done manually. When the problem is observed, the solution is to return to the
circuit diagram and lock the correct pin designations in place.
During the time of preparing
this book, there have been substantial improvements in computer-aided design
support. Following the successful completion of the original design at Bristol
University in 1991, the design files were made available to Direct Insight Ltd.
(U.K.). In 1993 the design was completed using NeoCAD software for Xilinx
FPGAs, and with the aid of a 50 MHz PC486 computer. The standard
placement-and-routing package was run with 100 cost tables. No timing
constraints were specified, and so the system ran without timing optimization.
After 108 hours, it had tried 64 cost tables, and one of these resulted in a
fully-routed chip, taking 1 hour and 25 minutes. Twenty-eight had less than 10
nets unrouted, and human intervention could probably have quickly resulted in
other fully-routed options. The fully-routed version was run through five
cost-based clean-ups and five delay-based clean-ups, taking a further 18
minutes. The design achieved a 6.3 MHz clock rate. Following further routing
iterations over 24 hours, the clock rate had increased to 7 MHz. This is
comparable with the existing design, which operates reliably at 6.75 MHz. A
layout for the final NeoCAD design is shown in
Figure 5–38.
In 1994 the current production release
of Xilinx software XACT 5.0.0 was run with XACT-Performance enabled, so that
the resulting circuit would run at its highest speed. After 82 hours on Sun
Microsystems SPARC 10 workstations, the system had generated 11 full-routed
designs out of 16 attempts. The first fully-routed result was available after 1
hour and 49 minutes. The varied results were produced by selecting different
placement parameters, including the placement “seed” and “placer effort.” The
clock rates for fully-routed chips varied from 5.4 MHz to 6.9 MHz. Six of the
11 fully-routed designs performed at 6.0 MHz or faster. The best two results
gave speeds of 6.8 and 6.9 MHz, which compare favorably with the existing
design (6.75 MHz). A layout for the fastest Xilinx design is shown in
Figure 5–39.
Figure 5–38 Final NeoCAD
design for the parallel controller.
5.7.4 Conclusions
The full 16-bit version of the
controller was eventually routed. While in 1991 this took over four months of
continuous effort, more recent CAD software allows rapid completion of quite
complex designs to specified performance criteria. An 8-layer printed-circuit
board has been designed and manufactured, and there are now more than 25 copies
of the design in routine use.
SUGGESTIONS FOR
PROJECTS
- Faster
adder circuits based on carry-lookahead logic [Wakerly90]. Note
that the Xilinx 4000 series incorporates carry-lookahead logic in its
CLBs.
- Arithmetic-logic
unit, (see [Wakerly90]).
- Design
an elementary processor, (see [Segee91]).
- Adapt
the sorter design for another FPGA family.
- Boundary
Scan. Boundary Scan testing has recently become standard, and considerably
simplifies testing both chips and their printed circuit board environment.
See [Maunder90] for
details.
- Dynamic
memory controller. Dynamic memory requires periodic refresh to avoid loss
of contents. For example, the Intel 4116 16K DRAM is organized as 128 rows
and 128 columns. Each row can be read and rewritten in a single cycle, and
each must be visited every 2 ms.
- Asynchronous
serial data transmission and reception. The RS232 standard defines start
and stop bits for the 8-bit characters. Using a clock running at 4 times
the nominal baud rate, it is possible to sample the incoming bits
correctly. The transmitter design is simpler than the receiver.
- Manchester-coded
data transmission. Manchester coding carries both data and timing
information on the same channel, and the edge transitions in each bit time
allow a receiver to adjust its clock by speeding up or slowing down from
the nominal bit rate. The receiver design calls for a phaselocked loop,
which can automatically adjust the sampling rate.

Figure 5–39. Final Xilinx
design for the parallel controller.